Mirley - Elektronika i Programowanie

Twierdzenia zawarte tutaj są konieczne podczas analizy obwodów liniowych, czyli takich które mogą być opisane równaniami liniowymi (algebraicznymi lub różniczkowymi).

1. Prawo Ohma

Prawo Ohma mówi, że spadek napięcia na elemencie o rezystancji R jest wprost proporcjonalny do natężenia prądu płynącego przez ten element.

Można to przedstawić jako:

$$ I \sim U $$

Współczynnikiem proporcjonalności jest : $ G = {\frac 1 R} $ , gdzie G jest konduktancją.

$$I = {\frac U R} = GU$$

Powyższe prawo jest słuszne gdy występują ustalone parametry przepływu prądu, szczególnie stała temperatura przewodnika. Gdy rezystancja R jest funkcją płynącego przez nią prądu nie możemy stosować tej prostej zależności (np. w półprzewodnikach)

Prawo Ohma w postaci różniczkowej:

$$ dI = \frac{dU}R $$

Prawo Ohma w wersji całkowej:

$$ I = \int_S \vec{j} \cdot d\vec{S} $$
gdzie: $ j = \frac{dI}{dS} $ jest gęstością prądu

2. I Prawo Kirchhoffa

Pierwsze Prawo Kirchhoffa mówi o tym że w każdym węźle obwodu elektrycznego suma algebraiczna wszystkich prądów jest równa 0. Umownie możemy przyjąć że prądy wpływające do węzła zapisujemy ze znakiem "+" a wypływające "-"

Powyższą treść wzorując się na rysunku zapisujemy wzorem:

$$I_1 +I_2 - I_3 - I_4 = 0 $$
lub $$I_1 +I_2 = I_3 + I_4$$

3. II Prawo Kirchhoffa

Drugie Prawo Kirchhoffa dotyczy bilansu napięć w zamkniętej części obwodu elektrycznego. Mówi o fakcie że w dowolnym oczku obwodu elektrycznego suma algebraiczna wszystkich napięć (zarówno źródłowych jak i spadków napięcia na odbiornikach) równa jest 0. Znaczymy umowny kierunek obiegu oczka przez co wszystkie napięcia zgodne z tym zwrotem piszemy ze znakiem "+" a przeciwne z "-"

Powyższą treść wzorując się na rysunku zapisujemy wzorem:

$$E_1 - U_1 - U_2 +E_3 - U_3 - E_2 = 0$$

korzystając z Prawa Ohma dla odbiorników(rezystorów) otrzymujemy:

$$E_1 - I_1R_1 - I_2R_2 +E_3 - I_3R_3 - E_2 = 0$$

4. Zasada Superpozycji

Zasada Superpozycji odnosi się do liniowych obwodów elektrycznych. Mówi o tym że odpowiedź obwodu na działanie kilku wymuszeń jest równa sumie odpowiedzi obwodu na każde wymuszenie z osobna. Dzięki tej zasadzie możemy analizować zachowanie obwodu dla każdego ze źródeł niezależnie, pomijając chwilowo wpływ pozostałych a następnie zsumować wyniki. Poniżej przedstawiony jest przykład na zastosowanie tego twierdzenia:

Obwód zawiera dwa wymuszenia(źródła), napięciowe E i prądowe I. Celem jest obliczenie prądu płynącego przez $R_L$:

Korzystając z Zasady Superpozycji liczymy najpierw prąd $I_L(E)$ związany ze źródłem napięciowym E, dezaktywując (rozwierając) źródło prądowe.

Traktujemy obwód jako dzielnik napięcia złożony z rezystora $R_1$ oraz równoległego połączenia $R_2$ z $R_L$ i obliczamy $U_2 = U_L$:

$$U_L = E \cdot \frac{R_2||R_L}{R_1 + R_2||R_L} = E \cdot \frac{\frac{R_2 \cdot R_L}{R_2 + R_L}}{R_1 + \frac{R_2 \cdot R_L}{R_2 + R_L}} = E \cdot \frac{R_2 \cdot R_L}{R_1 \cdot (R_2 + R_L) + R_2 \cdot R_L}$$

A zatem prąd $I_L(E)$ jest równy:

$$I_L(E) = \frac{U_L}{R_L} = \frac{E}{R_L} \cdot \frac{R_2 \cdot R_L}{R_1 \cdot (R_2 + R_L) + R_2 \cdot R_L}$$

Drugim krokiem jest obliczenie prądu $I_L(I)$ pochodzącego od źródła prądowego I po dezaktywacji (zwarciu) źródła napięciowego.

Traktujemy obwód jako dzielnik prądu złożony z rezystora $R_L$ oraz równoległego połączenia $R_1$ z $R_2$ i obliczamy $I_L(I)$:

$$I_L(I) = I \cdot \frac{R_1||R_2}{R_L + R_1||R_2} = I \cdot \frac{\frac{R_1 \cdot R_2}{R_1 + R_2}}{R_L + \frac{R_1 \cdot R_2}{R_1 + R_2}} = I \cdot \frac{R_1 \cdot R_2}{R_L \cdot (R_1 + R_2) + R_1 \cdot R_2} $$

Prądy $I_L(E)$ oraz $I_L(I)$ płyną w tym samym kierunku więc:

$$I_L = I_L(E) + I_L(I) = \frac{E}{R_L} \cdot \frac{R_2 \cdot R_L}{R_1 \cdot (R_2 + R_L) + R_2 \cdot R_L} + I \cdot \frac{R_1 \cdot R_2}{R_L \cdot (R_1 + R_2) + R_1 \cdot R_2}$$

5. Twierdzenie Thevenina
Dowolny liniowy obwód aktywny można od strony wybranych dwóch zacisków A i B zastąpić obwodem równoważnym złożonym z szeregowego połączenia źródła napięcia (o wartości równej napięciu między zaciskami A i B w stanie rozwarcia) i rezystancji zastępczej (równej rezystancji obwodu pasywnego widzianej od strony zacisków A i B)

Na rysunku poniżej przedstawiony jest przykład do tego twierdzenia:

W celu zastąpienia części obwodu (rysunek powyżej, "na lewo" od zacisków A i B) obwodem równoważnym musimy obliczyć wartość napięcia między zaciskami A i B oraz rezystancję tego obwodu widzianą od strony zacisków.

Na rysunku poniżej przedstawiony jest schemat zastępowanej części obwodu:

Napięcie $E_z$ najlepiej policzyć z zasady superpozycji:

$$E_z = E \cdot \frac{R_2}{R_1+R_2} + I \cdot \frac{R_1 \cdot R_2}{R_1 + R_2}$$

Natomiast rezystancja obwodu pasywnego jak na rysunku poniżej:

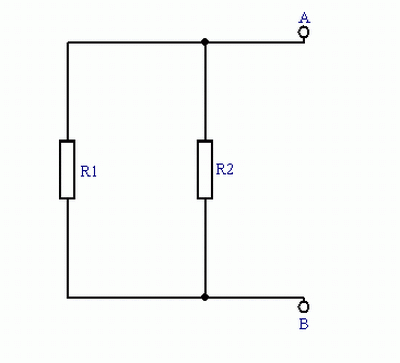
jest prostym połączeniem równoległym $R_1$ i $R_2$:

$$R_z = R_1||R_2 = \frac{R_1 \cdot R_2}{R_1 +R_2}$$

6. Twierdzenie Nortona

Dowolny liniowy obwód aktywny można od strony wybranych dwóch zacisków A i B zastąpić obwodem równoważnym złożonym z równoległego połączenia źródła prądu (o wartości równej prądowi płynącemu między zaciskami A i B w stanie zwarcia) i rezystancji zastępczej (równej rezystancji obwodu pasywnego widzianej od strony zacisków A i B)

Na rysunku poniżej przedstawiony jest przykład do tego twierdzenia:

W celu zastąpienia części obwodu (rysunek powyżej, "na lewo" od zacisków A i B) obwodem równoważnym musimy obliczyć wartość prądu płynącego między zaciskami A i B w stanie zwarcia oraz rezystancję tego obwodu widzianą od strony zacisków.

Na rysunku poniżej przedstawiony jest schemat zastępowanej części obwodu:

Prąd $I_z$ liczymy korzystając z zasady superpozycji:

$$I_z = \frac{E}{R_1} + I$$

Natomiast rezystancja obwodu pasywnego jak na rysunku poniżej:

jest prostym połączeniem równoległym $R_1$ i $R_2$:

$$R_z = R_1||R_2 = \frac{R_1 \cdot R_2}{R_1 +R_2}$$